スポンサーリンク
どーもー！！ナツです！！
今日はどうしたのー？
今日はどうしたのー？
サンプルサイズの根拠は？って言われたんだけど、サンプルサイズに根拠とかあるの？
研究計画を立てるにあたって考えるべき重要なことにサンプルサイズがあります。
適切なサンプルサイズでないと研究結果の信憑性が下がってしまうし、論文などで報告する時にはサンプルサイズの根拠を求められることだってあります。
でも、サンプルサイズの重要性は理解していてもサンプルサイズそのものについてはあまり理解できていないのではないでしょうか。
サンプルサイズを決めることは必要だと思っていても、決め方が分からずに何となくデータを取ってしまっていたり、論文を書くときに慌ててサンプルサイズを計算してみたりしていませんか。
この記事ではサンプルサイズについて良く理解できていない人、サンプルサイズを計算する方法が知りたい人に向けて、サンプルサイズの基礎知識とサンプルサイズを決める必要性、無料のサンプルサイズ計算ソフトについて解説していきます。
この記事を読むことで、サンプルサイズについて正しい知識を得ることができます。
それでは、解説していきます。
- サンプルサイズについて良く理解できていない人
- サンプルサイズを計算する方法が知りたい人
サンプルサイズとは
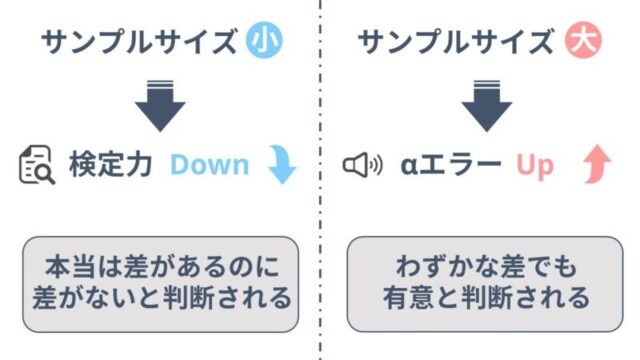
母集団から抽出した標本内のデータ数のことをサンプルサイズと呼びます。サンプルサイズは統計の結果に大きく影響し、一般的にサンプルサイズが小さいと有意と判断されにくくなり、反対にサンプルサイズが大きすぎると本当は差がないのに差があると判断される確率が高くなってしまいます。
そのため、統計結果の信憑性を向上させるためには適切なサンプルサイズを計算する必要があり、研究結果を公表する際にはサンプルサイズの計算方法も併せて報告することが必要です。
母集団とは、研究で検証したい集団全体のことです。
例えば65歳以上の高齢者を対象にした研究であれば日本に住む65歳以上の高齢者全員が母集団となります。
研究結果を確実なものとするためには母集団全員を調査する全数調査という方法が最も確実ですが、現実的には困難な場合が多いと思います。
そこで、母集団から標本として対象者を抽出して、データ収集を行うという方法が一般的です。
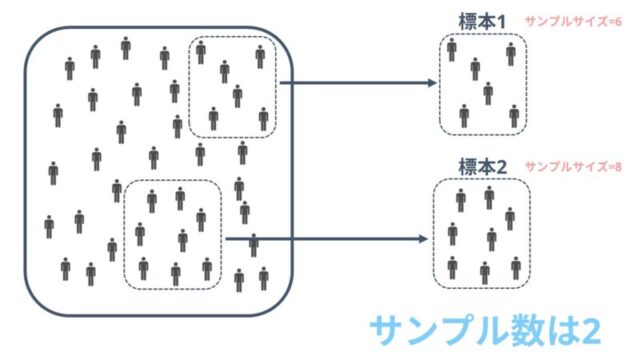
サンプルサイズと混同されやすい用語としてサンプル数があります。
サンプル数とは母集団から抽出した標本の数のことです。
「え？何が違うの？」と思われた方もいるかもしれませんが、全然違います。
先ほどの65歳以上の高齢者を対象とした研究を例に挙げると、A県、B県、C県からそれぞれ100名ずつランダムに抽出して研究を行った場合、サンプル数はA県、B県、C県の3になります。
サンプルサイズは各県100名ずつ抽出したため各100になります。
医学研究などで、介入群50名とコントロール群100名を抽出してデータ収集を行った場合は、サンプル数は2、サンプルサイズは介入群50、コントロール群100となります。
サンプルサイズとサンプル数は混同されやすいので注意してください。
サンプルサイズを決める必要性
サンプルサイズを決める理由は研究結果の信憑性を担保するためです。適切なサンプルサイズで出ない場合は統計の結果の信憑性が低くなってしまいます。
サンプルサイズが小さいと検定力が低くなってしまい、本当は差があるのに差がないと判断される確率が高くなってしまいます。
反対にサンプルサイズが大きすぎると、αエラーが大きくなり、ちょっとした差でも統計的に有意と判断されてしまいます。
どちらも真の結果を歪めてしまう原因となるため、適切なサンプルサイズを計算し、データを収集していく必要があります。
サンプルサイズを決めるために必要な知識
サンプルサイズを決めるにあたり、以下の3つを正しく理解しておきましょう。
- 効果量
- αエラー
- 検定力
効果量
効果量とは群間での平均値の差や関連性の強さを表した数値です。
一般に効果量が大きいほど検定力が高くなっていきます。
つまり、効果量を大きく設定すればそれだけ必要なサンプルサイズは小さくなっていきます。
効果量のだいたいの目安として、t検定では
-
効果量(小)：0.2
- 効果量(中)：0.5
- 効果量(大)：0.8 【Cohenのdの場合】
とされています。効果量の目安は以下の論文で詳しく記述されていますので、参考にしてみてください。
αエラー
αエラーとは本当は差がないにも関わらず、差があると判断されてしまう確率のことです。
αエラーとはp値と同じ意味で捉えられることもあり、一般的には0.05(5%)で計算されますが、よりαエラーを小さく設定したい研究の場合は0.01(1%)で計算される場合もあります。
どちらにせよ、サンプルサイズを計算する際には、有意水準をいくらにするかという考え方でOKです。
サンプルサイズ計算ソフトとして有名のはG-Powerです。
検定力
検定力とは本当に差がある場合に、正しく有意差があると判断される確率のことです。
検定力は1-βで計算され、βは本当は差があるのに差がないと判断されてしまう確率のことです。
βエラーという方が聞き覚えがある人もいるかもしれませんね。
βが0.2であれば検定力は0.8となります。
この場合、本当に差があるときには80%の確率で有意差があると判断されると解釈できます。
検定力は通常、0.8として計算されますが、根拠には乏しく慣例的に設定されているように感じます。
検定力は0.5などと下げても良いですが、その場合は必要なサンプルサイズは大きくなっていきます。
サンプルサイズ計算ソフト
サンプルサイズ計算ソフトとして有名のはG-Powerです。G-Powerは無料で使えるサンプルサイズ計算ソフトで論文でサンプルサイズの計算方法を報告する際にも多く使用されています。
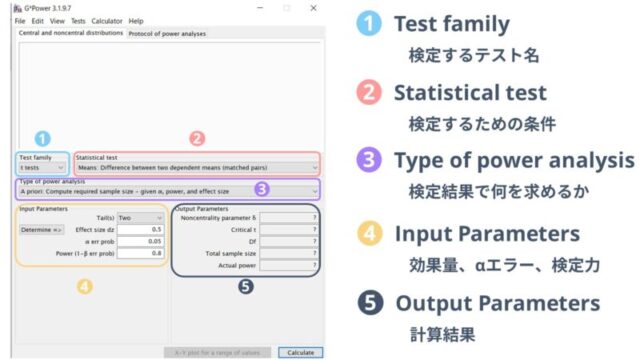
G-powerでできることは
-
研究前にサンプルサイズを計算する
-
検定結果から検定力を計算する
-
研究結果から効果量を計算する
などがあります。G-powerの画面はこんな感じになっています。
全て英語ではありますが、シンプルでとても使いやすいためとてもおすすめです。
僕自身もサンプルサイズを計算する時にはG-Powerを使っていますので、ぜひ使ってみてください。
また、G-Powerの詳細な使い方についても「【G-Powerの使い方】無料のサンプルサイズ計算ソフトの操作方法を画像付きで分かりやすく解説！！」で詳しく解説していますので、そちらもご覧ください。
まとめ
- サンプルサイズとは母集団から抽出した標本内のデータ数のこと
- サンプルサイズとサンプル数の混同に注意
- サンプルサイズを決める理由は研究結果の信憑性を担保するため
- 効果量、αエラー、検定力の知識を備える
- 無料のサンプルサイズ計算ソフトはG-Power
いかがだったでしょうか。
今回はサンプルサイズとその周辺知識についてまとめました。
サンプルサイズは研究の信憑性を担保するための重要な要素です。
近年は、徐々にサンプルサイズの計算方法についても報告されるようになってきましたが、それでもまだまだ報告が必須とまではなっていません。
サンプルサイズについて正しく理解して、研究発表の際には適切に報告するようにしましょう。
自分の研究の信憑性がぐっと上がり、研究者としてレベルアップできますよ。
この記事がサンプルサイズで悩んでいる人の手助けになればうれしく思います。
スポンサーリンク
