スポンサーリンク
どーもー！！ナツです！！
今日はどうしたのー？
今日はどうしたのー？
サンプルサイズの計算にG-Powerってソフトを使ってるんだけど、使い方がよく分かんないんだ
皆さん、研究を始める前にサンプルサイズを計算しているでしょうか。
ヒトを対象した研究の場合は協力いただける人数の関係上、どうしてもサンプルサイズが小さくなりやすかったり、特に計算もせずに取れたデータで分析してしまったりしていることも多いと思います。
ところが、近年は論文で発表する際にサンプルサイズの根拠を求められることが多くなっています。
サンプルサイズに根拠を持たせて報告することは研究の信憑性を向上させるというとても大きなメリットがありますが、実際、どのようにすれば計算できるのか分からない人も多いのではないでしょうか。
サンプルサイズの計算には無料検定力ソフト「G-Power」をお勧めします。
ここまでのことを無料でできるのかーってくらい優良なソフトです。
ところが、「G-Powerは全て英語で書かれていて、よく分からない」、「何をどういじればサンプルサイズが計算できるのか分からない」って人もいるのではないでしょうか。
この記事では、G-Powerを使ったサンプルサイズの計算方法について、分析方法別に実際の画面を見ながら解説していきます。
この記事を読むことで、自分の研究に必要なサンプルサイズをG-Powerを使って簡単に計算できるようになります。
サンプルサイズの基礎知識や重要性については下の記事で詳しく解説していますので、そちらを見てからこの記事を読んでもらうとより理解できると思います。
それでは解説していきます。
G-powerとは無料で使用できる検定力分析ソフトです。
G-Powerで主に使われている分析は以下の3つです。
G-Powerはハインリッヒ・ハイネ大学で開発され、同大学のホームページからダウンロードすることができます。
- サンプルサイズを無料で計算する方法が知りたい
- G-Powerの使い方を実際の画面を見ながら理解したい
関連記事一覧
Contents
G-Powerとは
G-powerとは無料で使用できる検定力分析ソフトです。検定力に関する種々の分析が可能なソフトですが、主に使用される分析は研究前のサンプルサイズの計算ではないでしょうか。
G-powerは非商業的プログラムとして開発され、無料でダウンロードして使用することができます。
サンプルサイズの算出根拠としてG-powerを使用したことを報告している論文も多く、十分に信頼性があるソフトといえます。
G-powerで何ができるのか
G-Powerで主に使われている分析は以下の3つです。
-
研究前にサンプルサイズを計算する
-
検定結果から検定力を計算する
-
研究結果から効果量を計算する
研究前にサンプルサイズを計算する
αエラー、検定力、効果量から必要なサンプルサイズを計算します。
研究にはサンプルサイズの根拠が必要で、サンプルサイズが小さすぎると検定力が低下し、サンプルサイズが大きすぎるとαエラーが増大します。
研究の信憑性を向上させるためにも、近年はサンプルサイズの根拠も報告することが求められるケースが多いように感じます。
検定結果から検定力を計算する
αエラー、効果量、サンプルサイズから検定力を算出します。
この分析は、過去に行われた研究がどの程度検定力があるかを検証する際に使用されます。
検定力とは１-βエラーで算出され、本当に差がある場合に、正しく差があると判断される確率です。
βエラーとは本当は差があるのに差がないと判断されてしまう確率のことで、βエラーが0.2(20%)だった場合、検定力は0.8(80%)となります。
この時は本当に差があるときには80%の確率で有意差があると判断されると解釈できます。
研究結果から効果量を計算する
αエラー、検定力、サンプルサイズから効果量を算出します。
効果量とは群間での平均値の差や関連性の強さを表した数値で、効果量が大きいほど検定力が高くなっていきます。
効果量の大まかな目安は以下のようになっています。
-
効果量(小)：0.2
-
効果量(中)：0.5
-
効果量(大)：0.8 【Cohenのdの場合】
効果量は有意差があっても、その差が本当に意味のある差なのかどうかを判断する指標になります。
有意差があっても効果量が低い場合は、意味のない差である可能性が出てきます。効果量については、以下の論文がとても参考になるので、ぜひ読んでみて下さい。
G-Powerのダウンロード
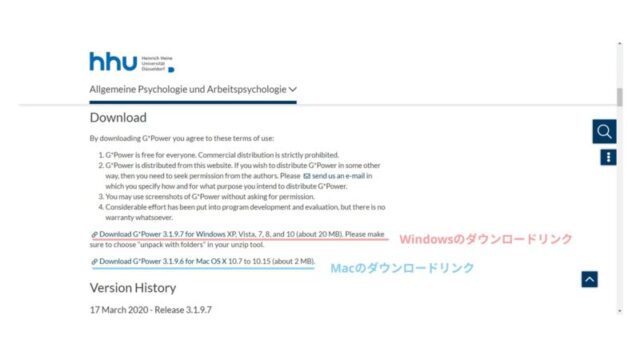
G-Powerはハインリッヒ・ハイネ大学で開発され、同大学のホームページからダウンロードすることができます。下にリンクを張っていますので、そちらからダウンロードしてください。
ダウンロードリンクが少し下の方にありますが、リンクの色が分かりにくいので注意してください。
ダウンロードが完了したら、ファイルを起動してインストールを行います。
インストールは数分で完了し、インストール後は自動的にデスクトップにアイコンが表示されるようになります。
もし、デスクトップにない場合はPC内検索で「GPower」(ハイフンなし)と検索してみてください。
G-powerの操作方法
G-powerを起動した際の画面はこのようになっています。
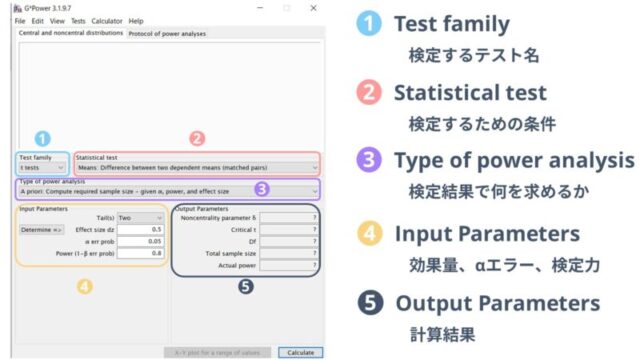
この内、入力する必要のある項目は
- Test family
-
Statistical test
-
Type of power analysis
-
Input Parameters
の4か所です。⑤Output parametersには計算の結果が出力されるので、特に触る必要はありません。
Test family
Test familyの項目では、検定するためのテスト名を入力します。
この内、主に使用するのは「t test」と「F test」だと思います。
「t test」では、2群間の比較検定に関する計算を行いま、「F test」では分散分析などの3群間以上の比較検定に関する計算を行います。
ここでは、あくまでテスト名を選ぶだけで、その後の細かい条件は次のStatistical testの項目で入力していきます。
Statistical test
Statistical testの項目では、より細かい検定条件の入力を行っていきます。
「t test」では、対応のあるt検定、対応のないt検定、Wilcoxon検定、Mann-Whitney検定、相関分析などの指定ができます。
「F test」では一元配置分散分析、２元配置分散分析、反復測定分散分析などの指定が可能です。
Type of power analysis
Type of power analysisの項目では検定結果で何を算出するかを入力します。
サンプルサイズを計算したい場合は「A priori：～」を選択します。
また、研究結果から検定力を算出したい場合には「Post hoc：～」を選択してください。
効果量の算出の場合は「Sensitivity～：」を選択します。
Input Parameters
Input Parametersの項目では、効果量、αエラー、検定力を入力します。
これらはサンプルサイズの計算において事前に検討しておく必要があります。
それぞれどのような値を入力するべきかについては、過去記事【サンプルサイズの決め方】基礎知識や必要性、無料の計算ソフトについて分かりやすく解説！！を参考にしてください。
Output parameters
Output parametersには計算の結果が出力されます。
「sample size」の項目に必要なサンプルサイズが書かれています。
先にも書きましたが、サンプルサイズは小さすぎても、大きすぎても結果に歪みを生じさせます。
可能な限り出力された最適なサンプルサイズに収まるようにデータを収集してください。
G-powerによる実際の分析
ここでは、サンプルサイズの計算方法について、以下の3つのパターンを画像付きで解説していきます。
- 2群間のパラメトリック検定
-
2群間のノンパラメトリック検定
-
相関分析
-
一元配置分散分析
2群間のパラメトリック検定
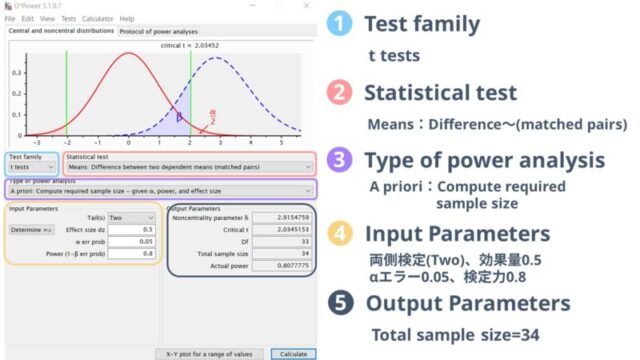
2群間のパラメトリック検定では「対応のあるt検定」と「対応のないt検定」のサンプルサイズの算出方法を解説します。
実際に「対応のあるt検定」で行った際の画面はこのようになります。
Input Parametersで、両側検定（two）、効果量0.5、αエラー0.05、検定力0.8で計算した結果、必要なサンプルサイズは34と計算されました。
続いて「対応のないt検定」で行った画面はこのようになります。
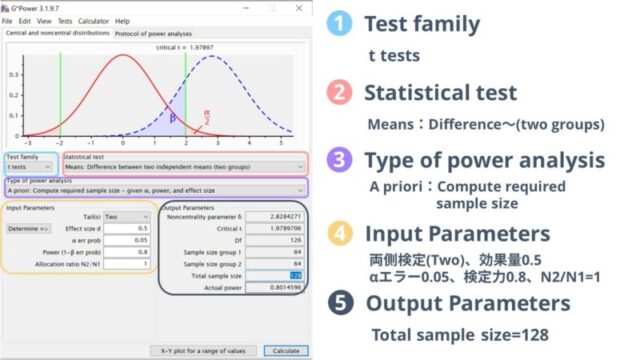
こちらも両側検定（two）、効果量0.5、αエラー0.05、検定力0.8で計算した結果、必要なサンプルサイズは各群64名ずつ、合計128名と計算されました。
また、Input ParametersのN2/N1とは各群の人数比率のことです。
今回はN2/N1を1としていますので、各群が同数で算出されますが、同数のサンプルが用意できない可能性がある場合はその比率を入力してください。
t検定の選択方法については過去の記事「【t検定の選び方】対応のある？対応のない？適切な選び方を徹底解説！！」で解説していますので、そちらも併せて見てみて下さい。
2群間のノンパラメトリック検定
2群間のノンパラメトリック検定では、「Wilcoxon検定」と「Mann-Whitney検定」のサンプルサイズの算出方法を解説します。
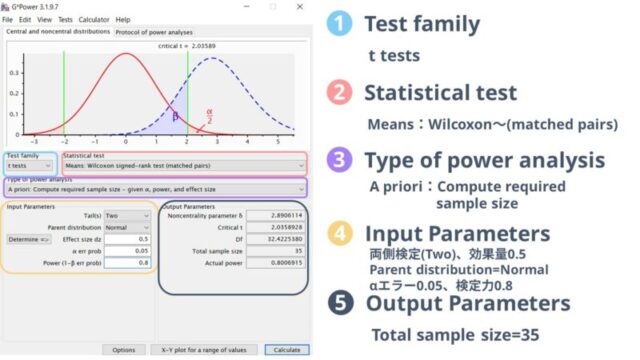
まずは「Wilcoxon検定」から見ていきましょう。
「Wilcoxon検定」で行った場合の画面はこのようになります。
両側検定（two）、効果量0.5、αエラー0.05、検定力0.8で計算した結果、必要なサンプルサイズは35と計算されました。
この時、Parent distributionの箇所はNormalを設定しておいて大丈夫です。
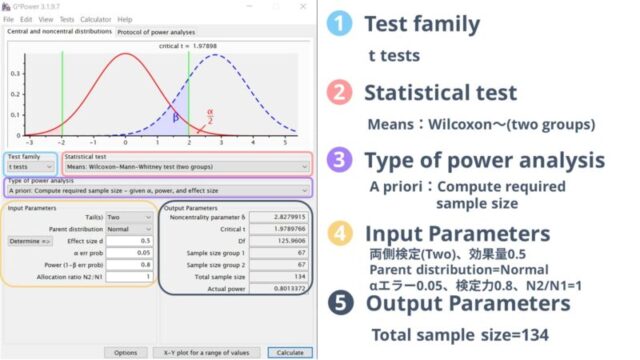
続いて、「Mann-Whitney検定」の場合を見てみましょう。
「Mann-Whitney検定」でサンプルサイズを計算した場合はこのようになります。
こちらも両側検定（two）、効果量0.5、αエラー0.05、検定力0.8、N2/N1比を1として計算した結果、必要なサンプルサイズは各群67名ずつ、合計134名と計算されました。
この時もParent distributionの箇所はNormalを設定しておけば大丈夫です。
相関分析
相関分析では、「Pearsonの積率相関係数」と「Spearmanの順位相関係数」のサンプルサイズの計算方法を解説します。
パラメトリックとノンパラメトリック、どちらも同じ操作で計算が可能なので、区別する必要はありません。
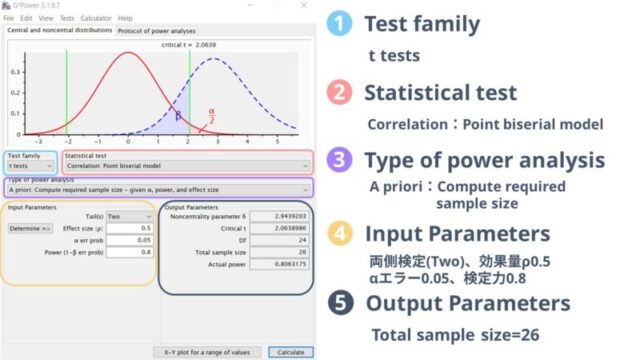
また、相関分析では効果量として期待する相関係数を入力する必要があります。
G-Powerでは相関分析の効果量に小(0.1)、中(0.3)、大(0.5)を推奨されていますが、数値は自由に変更することが可能です。
実際に計算を行った画面はこのようになりました。
両側検定（two）、効果量(相関係数ρ)0.5、αエラー0.05、検定力0.8として計算した結果、必要なサンプルサイズは26と計算されました。
また、相関分析については過去の記事「【相関係数とは？】検定方法や目安、結果の解釈の注意点などまとめて分かりやすく解説します！！」で詳しく解説していますので、そちらも併せてご覧ください。
一元配置分散分析
一元配置分散分析のサンプルサイズを計算する方法を解説していきます。
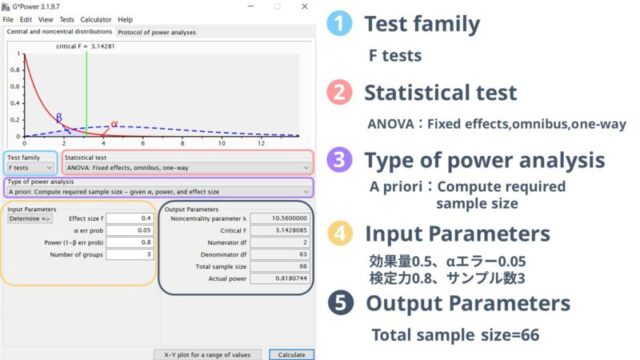
これまでと違い、Test familyの項目で「F test」を選択してください。
また、一元配置分散の効果量は小(0.1)、中(0.25)、大(0.4)が推奨されていますが、こちらも研究者が自由に設定することが可能です。
実際の画面はこのようになりました。
効果量0.4、αエラー0.05、検定力0.8、サンプル数3で計算した結果、必要な合計サンプルサイズは66と計算されました。
今回は3群間で指定していますので、3で割って各群に22名ずつサンプルが必要ということになりました。
まとめ
- サンプルサイズを計算するための無料ソフトはG-powerがおすすめ
- αエラー、検定力、効果量から必要なサンプルサイズを計算する
- G-Powerはシンプルで使いやすく、信頼性も高い
いかがだったでしょうか。今回はG-Powerを使ったサンプルサイズの計算方法について、実際の画面を見ながら解説しました。
G-Powerは本当にシンプルで使いやすく、無料で使えるのが噓のような素晴らしいソフトです。
その反面、操作画面が全て英語のため、「使いたいけど使い方が分からない」という人もいるのではないでしょうか。
G-powerを使って事前にサンプルサイズを計算したうえで、データ収集に臨みましょう。
そして、論文を書く際にはぜひサンプルサイズの根拠も併せて報告してください。
また、G-powerなど統計ソフトを使用するにはある程度のパソコンのスペックが必要です。
ノートパソコンの記事も書いていますので、そちらも見てみてください。
この記事がサンプルサイズで困っている人の助けになれば幸いです。
最後にサンプルサイズについてもっと詳しく知りたいという人は以下の書籍を参考にしてみてください。
少し古い本ですが、サンプルサイズだけでなく、様々な視点から研究について考察されています。
リンク
スポンサーリンク
