スポンサーリンク
どーもー！！ナツです！！
今日はどうしたのー？
今日はどうしたのー？
統計の結果を見てもらったんだけど、「正規性は見たのか？」って言われて。
正規性って見なきゃいけないの？
正規性って見なきゃいけないの？
データを取り終えて解析を始めると、統計手法の選択や実際の解析方法、結果の解釈など多くの壁にぶつかりますよね。
この複雑さが統計に苦手意識を持たせる原因なのかもしれませんが、その中でもデータの正規性について指摘されたことはありませんか。
パラメトリック検定を選択したら「データの正規性はちゃんと確認したのか」と言われ、ノンパラメトリックデータを選択してもやはり正規性について指摘されて…。
この時初めて正規性について正確に理解できていないことに気づいた人もいるかもしれません。
ところが正規性について調べてみると、難しい言葉や複雑な数式がたくさん出てきて、結局よく分からなかったなんてことも多いと思います。
この記事では、正規性について正しく理解したい人や統計に正規性がどう関わってくるのかを知りたい人に向けて、正規性とは何か、統計に正規性がどう関わってくるのかを難しい言葉や数式は一切に抜きにして解説していきます。
この記事を読むことで、統計において正規性をどの様に考えるべきかを理解することができ、統計手法の選択がスムーズに行えるようになります。
それでは解説していきます。
- 正規性について正しく理解したい人
- 統計に正規性がどう関わってくるのかを知りたい人
- 正規性を調べていると難しい数式が出てきて嫌になった人
統計について勉強している人は以下の記事で初心者向けの統計に関する書籍も紹介していますので、そちらもぜひ読んでみてください。今回解説している正規性についても理解も深まると思いますよ。
あわせて読みたい
正規性とは何か
正規性とはあるデータが正規分布に従っていることを指し、この記事では正規分布と同じ意味で使用することにします。正規分布とは自然界で最もありふれた確率分布であり、自然界の多くのデータが正規分布に従うことから英語ではnormal distributionと呼ばれています。
下のグラフを見てください。正規分布をグラフに表すとこのようになります。
統計手法の選定が目的で正規分布を勉強している人はこの「統計にどう関わってくるのか」が最も知りたい内容ではないでしょうか。
次は正規分布であるかどうかを確認する方法を3つ紹介します。
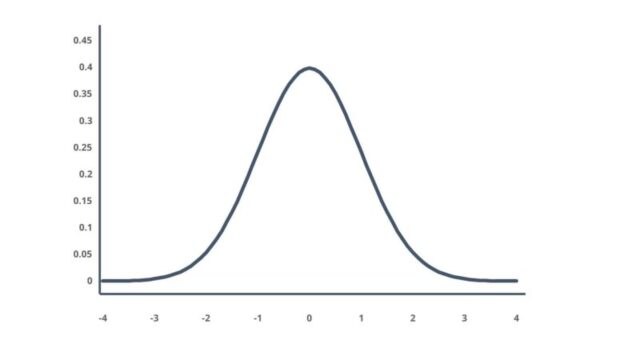
このグラフでは横軸は確率変数、縦軸は確率密度です。
難しい言葉が出てきましたが大丈夫です。
簡単に説明するとこんな感じです。
-
確率変数：データが取りうる値
-
確率密度：データがその値を取るであろう確率
100点満点のテストの点数を例に挙げると確率変数は0点～100点です。
確率密度は0点を取る確率や57点を取る確率になります。
この時、確率変数は0点から100点で固定されますが、確率密度はそのテストの難易度やテストを受けた人の属性などで変化します。
正規分布のグラフでは、平均値を中心に釣鐘状にデータが分布します。
一般的には比率尺度や間隔尺度は正規分布に従うとされており、反対に順序尺度や名義尺度は正規分布には従わないとされています。
正規分布のグラフの特徴
次に正規分布のグラフの特徴を解説していきます。
もう1度正規分布のグラフを見てみましょう。
平均値を中心に左右対称なグラフになっているのが分かると思います。
このため、そのデータは平均値を取る確率が最も高くなり、平均値からプラス方向であれマイナス方向であれ、遠くなればなるほどその値を取る確率は減少していきます。
そして正規分布のグラフにはもう一つ大きな特徴があります。
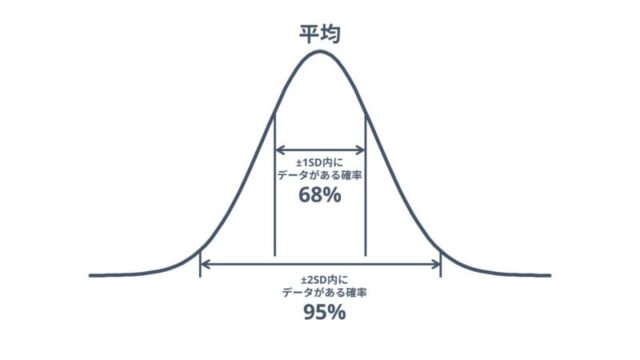
それは標準偏差でデータのばらつきが分かるという特徴です。
標準偏差とは平均身長156.6±7.9cmなどの表記があった場合の±以下の数値のことです。
この場合は7.9cmですね。
標準偏差は英語でStadard Deviationと表記され、SDと略されます。
標準偏差はデータのばらつきを表しており、平均値からプラスマイナスどのくらいの範囲にデータが収まっているかの参考になります。
標準偏差が大きいほどデータのばらつきが大きく、小さいほどデータのばらつきが小さくなっています。
正規分布の場合、平均値±1SDにデータのある確率が68%、平均値±2SDにデータがある確率が95%となっています。
平均身長156.6±7.9cmの場合148.7cm～164.5cm(平均値±1SD)までにデータのある確率が68%、140.8～172.4cm(平均値±2SD)までにデータがある確率が95%ということになります。
このように標準偏差を参考にしてデータのばらつきを知ることができるのは正規分布であることが前提となります。
正規分布でないデータの場合も、平均値±SDで表現されている場合もありますが、正規分布でないデータの場合はSDが大きくなりすぎている、すなわちデータのばらつき大きすぎるということになります。
正規分布でないデータの場合は中央値で表現するべきということも知っておいてください。
ちなみに平均値と中央値は過去の記事「【平均値と中央値について】それぞれの特徴と使い分けを具体例つきで徹底解説！！」で詳しく解説しているので、そちらも参考にしてみて下さい。
統計にどう関わってくるのか
統計手法の選定が目的で正規分布を勉強している人はこの「統計にどう関わってくるのか」が最も知りたい内容ではないでしょうか。結論から言うと、正規分布しているかどうかで選択するべき統計手法が変わります。
正規分布しているデータのことをパラメトリックデータ、正規分布していないデータのことをノンパラメトリックデータと呼びます。
2群間比較の例を挙げると、パラメトリックデータを比較したい場合は対応のあるt検定もしくは対応のないt検定を使用しますが、ノンパラメトリックデータを比較したい場合はWilcoxon検定もしくはMann-Whitney検定を使用します。
この時、パラメトリックデータの分析は正規分布していることを前提として計算されますが、ノンパラメトリックデータは正規分布しているかどうかは分からないという前提で計算されます。
実はこれが結構大切で、ノンパラメトリックデータで分析する場合は正規分布していても良いし、正規分布してなくても良いということになります。
極論ではありますが、すべてのデータをノンパラメトリックデータとして扱って解析していくこともOKですし、最近はそうしている研究も多くあります。
正規分布の確認方法
次は正規分布であるかどうかを確認する方法を3つ紹介します。
-
ヒストグラムを描く
-
Q-Qプロットを描く
-
正規性の検定を行う
ヒストグラムを描く
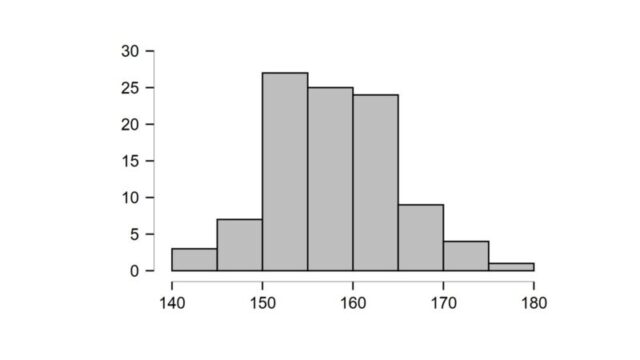
ヒストグラムとはデータをある区間ごとに区切り、各区間の個数や数値のばらつきを棒グラフ状で表現したグラフのことです。
ヒストグラムを描くことでデータの分布を視覚的に分かりやすく表現することができ、ヒストグラムが左右対称型になっていれば正規分布しているということができます。
ただし、ヒストグラムを描く方法で正規分布を確認した場合、その根拠となるのがグラフの目視となります。
目視である以上、本当に正規分布しているという根拠には乏しいように感じます。
Q-Qプロットを描く
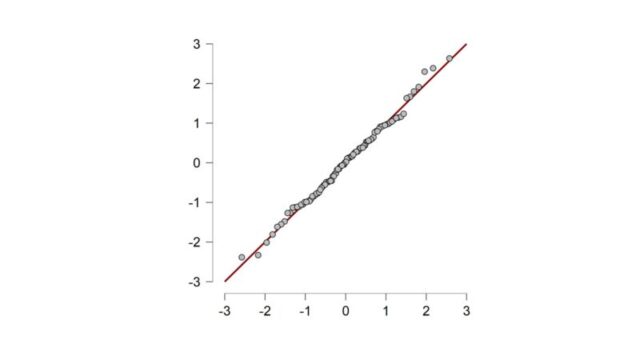
Q-Qプロットとは、データが正規分布に従う期待値を縦軸、データそのものの数値を横軸にとったグラフです。
Q-Qプロットが一直線上になれば正規分布しているということができますが、この場合も一直線かどうかは目視により確認します。
そのため、ヒストグラムと同様に数値的な根拠には乏しいと思ってください。
正規性の検定
正規性の検定を行う方法が正規分布かどうかを確認するもっとも一般的で確実な方法だと思います。正規性の検定には
-
Shapiro-Wilkの正規性検定
-
Kolmogorov–Smirnov検定
などがあります。
統計ソフトSPSSではShapiro-Wilkの正規性検定とKolmogorov–Smirnov検定が実施可能です。
一般的にデータ量が十分に多い場合にはKolmogorov–Smirnov検定、50件程度の少ないデータ量ではShapiro-Wilkの正規性検定を参考にしてください。
どちらの正規性の検定も帰無仮説は「データが正規分布している」となりますので、p値が0.05より大きい場合に正規分布していると解釈されます。
正規性の検定を行うときの注意点
正規性の検定を行うことで正規分布か否かを確認し、それによって統計手法の選択を行うことは先ほど説明しました。
でも、ここで一つ注意して欲しい点があります。
それは、多重検定性についてです。
多重検定性とは、検定を複数回実施することでαエラー(有意でないのに有意と判定してしまう確率)が増大してしまうことを指します。
正規分布の検定を行うということは、研究の中で検討すべきp値の数を増やすということになります。
そうすると、多重検定性の問題が生じ、研究全体を通してみるとαエラーを生じる確率が増大してしまいます。
近年はこの多重検定性の問題から、1つの研究内で検定するp値の数は必要最小限にする風潮が主流です。
そのため、そもそも正規性の検定を行わずに、ノンパラメトリックデータとして検定を行っていくことも考慮してみてください。
まとめ
- 正規性とはデータが正規分布に従っていること
- 正規分布のグラフは平均値を中心に左右対称になっている
- 正規性があるかどうかで選択すべき統計手法が変わる
- 正規性を確認するためには正規性の検定を行う
- 多重検定性の問題から正規性の検定は行わず、ノンパラメトリック検定を選択するのもOK
いかがだったでしょうか。今回は正規性について解説を行いました。
難しい数式などは一切に抜きにして解説しましたが、研究者が統計を行う上ではこの程度の知識で十分だと思います。
ただし、正規性の確認をするべきか、論文中にどう正規性の話を盛り込むかなどは正しい知識が必要です。
この記事が少しでも正規性について困っている人の参考になればうれしく思います。
スポンサーリンク
