研究を始めたばかりで統計に苦手意識を持っている人は多いと思います。
頑張ってデータを取って、「さあ解析を始めよう」としたときに尺度水準というわけ分からない言葉で出てきて途方に暮れている人もいるのではないでしょうか。
尺度水準とは数値データをその性質によって4つに分類したものです。
尺度水準を基に統計手法を決めていく場合もあり、統計の基礎的な知識として避けて通ることはできません。
この記事では、尺度水準をよく理解できない人、統計手法を決めるために自分のデータの性質を知りたい人に向けて、「尺度水準とは何か?」ということを実例を交えて分かりやすく解説します。
この記事を読めば、尺度水準を正確に理解することができ、統計手法を決めるための基本的な知識が身につきます。
初めて研究をする人、統計に悩んでいる人などはぜひ最後まで読んでいってください。
統計について勉強している人は以下の記事で初心者向けの統計に関する書籍も紹介していますので、そちらもぜひ読んでみてください。今回解説している尺度水準についても理解も深まると思いますよ。
尺度水準とは
尺度水準とはデータが持つ情報の性質に基づき、統計学的に分類したものを言います。
簡単に言うと
「データをその特徴に合わせて4つに分類しましょう」
ってことです。
その4つの分類とは以下のようなものになっています。
なぜ、尺度水準が必要になるかというと、尺度水準が何に該当するかによって採用する統計手法が変わるからです。
少し専門的になりますが、具体的な例を挙げると
- 間隔尺度の差の検定を行いたい⇒対応のあるt検定、対応のないt検定
- 順序尺度の差の検定を行いたい⇒Wilcoxon検定、Mann-Whitney U検定
このような感じで統計手法を選んでいきます。
もちろんこれ以外にも考慮することはありますがまずは尺度水準で手法が変わるということを理解して下さい。
実際の統計手法の選択については、以下の記事も参考にしてみてください。
次はそれぞれの特徴を見ていきましょう。
名義尺度
名義尺度とはデータを区別するためにつけた数値のことをいいます。
具体的には
- 性別:男性=1、女性=2とする
- 血液型:A型=1、B型=2、O型=3、AB型=4とする
などがあります。
名義尺度で使用する数字は何でも良くて、上の性別の例では「男性=0、女性=1」としても良いわけです。
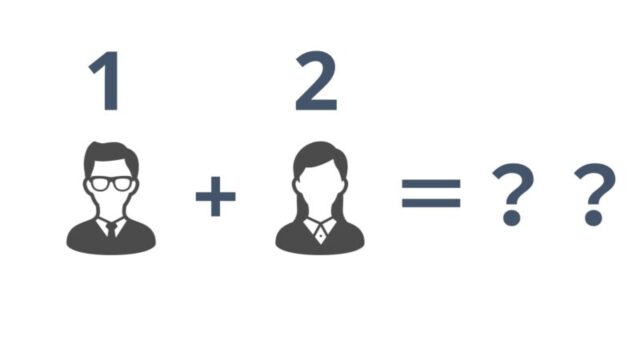
名義尺度には、数値の大小に意味はなく、四則演算(+、-、×、÷)が不可能であるという特徴があります。
1(男性)+2(女性)=3(??)
こんな足し算に意味はないですよね。

順序尺度
順序尺度とはデータの大小に意味はあるけれどその間隔が一定ではない数値のことをいいます。
具体的な例を挙げると
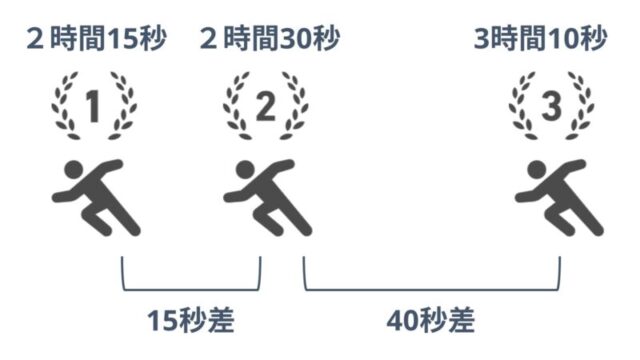
- マラソンの順位:1位、2位、3位・・・
- 心理尺度の結果:1点(全く当てはまらない)・・・5点(全く当てはまる)
こんな感じです。
順序尺度にはデータの大小関係に意味がありますのでマラソンの1位は2位よりも優れていますし、心理尺度の5点は1点よりも質問項目に当てはまっているということが出来ます。
一方で、数値同士の間隔が一定ではないという特徴もあります。
マラソンの例でいうと、1位と3位の中間が2位であるとは限りません。
1位がぶっちぎりで2位と3位が僅差の場合や1位と2位が僅差で、だいぶ遅れて3位の場合だってあります。
このため、四則演算を行ことはナンセンスですし、平均値も意味を持ちません。
ちなみに順序尺度の場合は中央値を使うことが推奨されています。
平均値と中央値の違いについてもこのブログで解説しているので併せてご覧ください。

間隔尺度
間隔尺度はデータの大小関係とその間隔の差に意味があるけれど0は相対的な意味しかもたない数値のことをいいます。
少し分かりにくいですね。
間隔尺度の代表として挙げられる数値に温度があります。
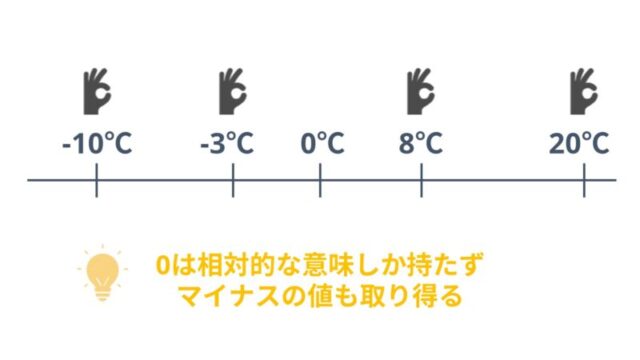
気温10℃と気温30℃では「30℃の方が20℃高い」と言うことが出来ますよね。
順序尺度では出来なかった足し算や引き算が意味を持つようになってきました。
また、「0が相対的な意味しかもたない」というのは「0=ない」とならないということです。
気温0℃はあり得ますし、マイナスになることもあります。
この様にマイナスの値をとるのも間隔尺度の特徴です。
一方、間隔尺度では掛け算や割り算は出来ないとされています。
それは、「30℃は10℃の3倍暑い」とは言えないということです。
これはイメージに近いですし、深くは知らなくて良いと思います。
とりあえず、差が等間隔で0は無ってことではないことを理解できれば十分です。

比率尺度
比率尺度はデータの大小関係とその間隔の差に意味があり0が絶対的な意味をもつ数値のことをいいます。
長さなどをイメージすると分かりやすいと思います。
また、間隔尺度では出来なかった掛け算や割り算も意味を持つようになってきます。
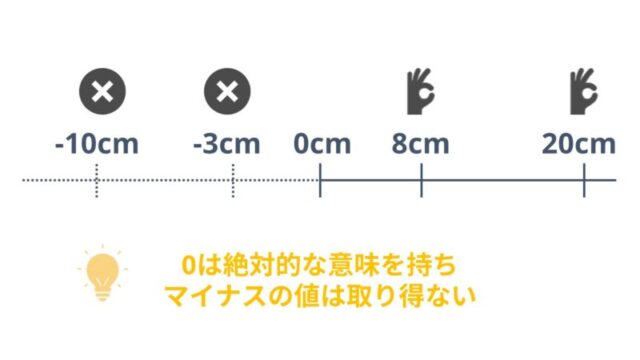
10cmと30cmは30cmの方が20cm長くて、3倍の値である
こんなことが比率尺度では言えるようになります。
また、0が絶対的な意味を持ちますので「0=ない」となります。
長さ0cmってそれは存在しないってことですよね。
そんなイメージです。
ちなみに
統計手法の選択のために尺度水準を勉強してる方は間隔尺度と比率尺度の区別は必要ありません。
この2つは同じ手法で分析されるからです。
自分の持つデータが
この3種類のどれに分類されるかを鑑別出来れば十分です。

統計手法の選び方
なぜ尺度水準を考えなければいけなかったかというと、尺度水準によって統計手法が変わるからでした。
実はこれは正確ではなく、「データが正規分布しているかどうかで統計手法が変わる」というのが正しい解釈です。
一般的には以下のように考えられています。
| 名義尺度 |
非正規分布 |
| 順序尺度 |
非正規分布 |
| 間隔尺度 |
正規分布 |
| 比率尺度 |
正規分布 |
このように、一般的には名義尺度と順序尺度は正規分布していない、間隔尺度と比率尺度は正規分布しているとされています。
正規分布についての詳細な解説は過去の記事「【正規性とは?】正規分布の特徴や統計に関わる考え方を数式なしで分かりやすく解説!!」を参考にしてください。
ただし、少ないデータ数では間隔尺度が正規分布していなかったり、反対に順序尺度なのに正規分布しているといったことも考えられます。
そして、尺度水準だけを見て統計手法を決めてしまうと、正規分布していないデータをパラメトリックな手法で分析してしまい、誤った結果を算出してしまうことになります。
そのため、尺度水準を考えるだけでなく、データが正規分布しているのかどうかという視点を持ってデータを解析するようにしてください。
正規分布についての正しい理解を得たら、次は統計手法の選定です。
統計手法の選定にはもう1つ必要な知識があります。それは、「対応があるデータか対応のないデータか」ということについてです。
対応についても過去の記事「【t検定の選び方】対応のある?対応のない?適切な選び方を徹底解説!!」で解説していますので、そちらを参考にしてください。
「正規分布しているかどうか」、「対応があるかどうか」の2つが理解できれば統計手法は簡単に選択することができます。以下の表を参考にして、統計手法を決めてみてください。
| |
パラメトリックデータ |
ノンパラメトリックデータ |
| 対応のあるデータ |
対応のあるt検定 |
wilcoxon検定 |
| 対応のないデータ |
対応のないt検定 |
Mann-Whitney検定 |
適切な統計手法の選択ができれば、あとは統計ソフトがすべて自動で計算してくれます。
現在は統計ソフトもたくさん開発されていて、無料でダウンロード可能な統計ソフトも豊富です。
このブログでは、おすすめの無料の統計ソフトやその使い方も解説していますので、そちらもぜひ見てみてください。
本当に簡単に統計を行うことが可能で、研究者の強い味方になると思いますよ。
まとめ
【名義尺度】
データを区別するためにつけた数値(性別、血液型など)
【順序尺度】
データの大小に意味はあるが、その間隔が一定ではない数値(順位、心理尺度など)
【間隔尺度】
データの大小関係とその間隔の差に意味があるが、0は相対的な意味しかもたない数値(温度、西暦など)
【比率尺度】
データの大小関係とその間隔の差に意味があり、0が絶対的な意味をもつ数値(長さ、身長、体重など)
いかがだったでしょうか。今回は尺度水準について解説をしました。
上でも少し書きましたが、間隔尺度と比率尺度の鑑別は正直必要ありません。
ただし、データとしての性質が異なっていることは理解して、統計手法の選択へ進みましょう。
また、研究を行うにはある程度のパソコンのスペックが必要です。
ノートパソコンの記事も書いていますので、そちらも見てみてください。