スポンサーリンク
どーもー！！ナツです！！
今日はどうしたのー？
今日はどうしたのー？
相関係数ってのを求めてみたいんだけど、正直よく分かってないんだ…
詳しく教えてくれない？
詳しく教えてくれない？
学会や論文ではよく相関係数を用いて成果発表がされていると思います。
差の検定と同じく、基本的な統計手法の1つですし、研究疑問を解決する手法としてよく選択されています。
ところが、相関係数についてどの程度理解しているでしょうか。
相関係数は初歩的な手法ではありますが、実は落とし穴もいくつかあります。
これらを正しく理解していないと結果の解釈を誤ってしまったり、間違った情報を発信してしまうことに繋がります。
この記事では、これから相関係数を用いて分析をしようとしている人、相関係数についてもう1度正しく理解したい人に向けて、相関係数の概要や目安、さらには検定方法と注意点も分かりやすく解説していきます。
この記事を読めば、相関係数についての正しい知識を得ることができ、相関係数についての分析はもちろん、結果の解釈も正しく行えるようになります。
いつも通り、難しい数式は一切抜きにしていますので、理解しやすいと思います。
それでは解説していきます。
- これから相関係数を用いて分析をしようとしている人
- 相関係数について正しく理解したい人
統計について勉強している人は以下の記事で初心者向けの統計に関する書籍も紹介していますので、そちらもぜひ読んでみてください。今回解説している相関係数についても理解も深まると思いますよ。
あわせて読みたい
相関係数とは
相関係数とは2つのデータの関係性を表す数値です。相関係数はアルファベットの「r」で略され、「一方が高いともう一方も高い」などの2つのデータの変動についての関係性の強さを表しています。
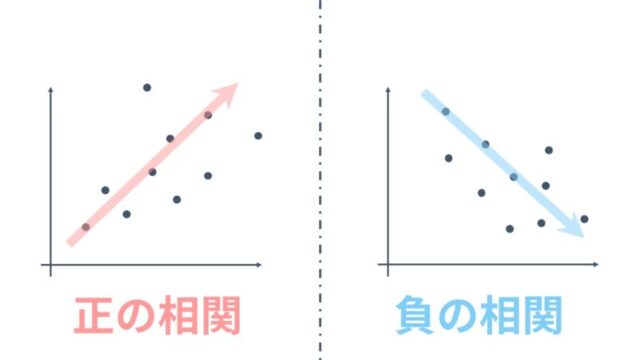
相関係数は-1～1までの間の数値をとり、プラスであれば正の相関関係、マイナスであれば負の相関関係と呼ばれています。
正の相関であれば「一方が高ければ、もう一方が低い」、負の相関であれば「一方が低ければもう一方は高い」と解釈できます。
相関係数の目安
相関係数は-1～1までの値をとりますが、相関係数が1.0に近ければ近いほど、強い相関関係を示しています。極端な話ですが、相関係数1.0であれば、それは同じものであるということができます。
余談ですが、心理尺度を用いた研究の世界では、項目同士の相関係数が高すぎると同じものを測定していると見なされてしまい、項目の妥当性が低いとされてしまいます。
相関係数に明確な基準は実はなく、研究者がそれぞれ別の文献を引用して決めている節があります。
ただし、一般的な基準は存在し、
-
～0.20 相関なし
-
0.20～0.40 弱い相関
-
0.40～0.70 相関あり(中等度の相関)
-
0.70～ 強い相関
などとされています。
この文言や数値もやはり研究によって微妙に異なりますが、だいたいこのくらいと理解しておいてください。
相関係数の検定
相関係数は共分散をそれぞれの変数の標準偏差で除すことで求められます・・・。一応計算方法をお伝えしましたが、研究者としてデータ処理に相関係数を用いる場合は細かい計算方法など理解する必要はありません。
今は統計ソフトが一瞬で、しかも正確に行ってくれますので、研究者に必要なのはむしろ統計を扱うための知識だと思います。
その知識として必要なのが2種類の相関係数についてです。
相関係数には
-
Peasrsonの積率相関係数
-
Spearmanの順位相関係数
があります。
比べたいデータが2つともパラメトリックデータの場合はPeasrsonの積率相関係数、比べたいデータのどちらか一方、もしくは両方ともノンパラメトリックデータの場合はSpearmanの順位相関係数を選択してください。
ただし、Spearmanの順位相関係数は非正規分布を前提としているわけではなく、分布は分からないことを前提として計算を行っています。
そのため、正規分布しているパラメトリックデータ同士でもSpearmanの順位相関係数での検定は可能です。
近年は多重検定性の問題から正規性の検定は行わず、全てノンパラメトリックデータとして分析するという考え方もあります。
そのあたりの話も過去に解説しているのでそちらも併せてご覧ください。
【正規性とは？】正規分布の特徴や統計に関わる考え方を数式なしで分かりやすく解説！！
データを取り終えて解析を始めると、統計手法の選択や実際の解析方法、結果の解釈など多くの壁にぶつかりますよね。
この複雑さが統計...
ちなみに、最近では相関係数の検定として、順序尺度×順序尺度ではポリコリック相関、順序尺度×連続尺度ではポリシリアル相関が行われるようになってきています。
細かい内容は割愛しますが、より真の値に近い相関係数が算出される手法です。
最近は無料の統計ソフトで検定ができるようになってきていますので、ぜひそちらの手法で行うことも考えてみて下さい。
相関係数とp値の話
統計ソフトで相関係数を算出すると、同時にp値も算出されます。このp値はどのように解釈するべきなのでしょうか。相関係数が0.38，p値が0.04の場合を例に挙げて解説します。
この場合は
相関関係がないという帰無仮説が採択される確率が4%であり、その場合の相関係数は0.38である
と解釈されます。
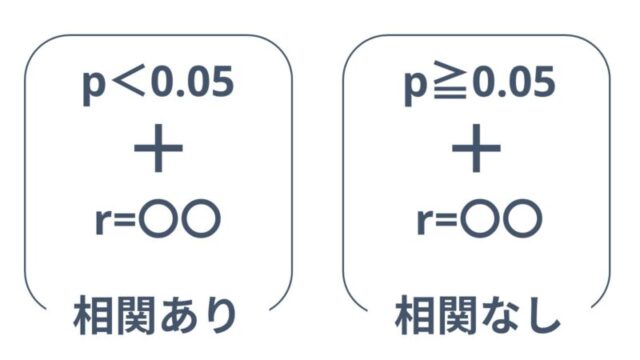
そもそも帰無仮説が棄却されなくては相関関係にあるということはできません。
つまり、p値が有意でない場合、相関係数が高くても相関はないと判断しなくてはならないということです。
このあたりは相関係数で勘違いされやすい部分だと思いますので、正しく理解しておいてください。
相関係数の解釈時の注意点
相関係数を解釈する際にはもう少し注意しなければならないことがあります。それは、原因と結果の方向については分からないという点です。
例えば勉強のやる気と成績について考えてみましょう。
この時、相関係数が正で有意だったとすると
「やる気の高い人は成績が良い」
と判断しますよね。
これは勉強のやる気を原因、成績を結果として捉えていますし、一見正しく見えます。
ところが、この原因と結果は逆の解釈でも成り立つ場合があります。
「成績が良いから勉強を面白く感じ、やる気が高い」
こう捉えることも十分可能だと思いませんか。
これが原因と結果の方向については分からないということです。
もちろん分かる場合もあります。
それは年齢と身長のように、どちらか一方が生物的にだったり物理法則的にだったりして普遍的である場合です。
真の関係性を知るためには縦断研究を行ったり、共分散構造分析を用いる必要がありますが、なかなか難しい場合もあるので、そのあたりの統計の限界は理解して結果を解釈して下さい。
まとめ
- 相関係数とは2つのデータの関係性を表す数値
- 相関係数0.2以上で相関があると判断できる
- 相関の検定にはPeasrsonの積率相関係数かSpearmanの順位相関係数を用いる
- p値が有意でない場合、相関係数が高くても相関はない
- 相関係数では原因と結果の関係性の解釈に注意が必要
いかがだったでしょうか。
今回は相関係数について解説しました。
特に最後に話した解釈については勘違いしている人、理解していない人も多いように感じます。
データの分析も大切ですが、結果を解釈して世の中に役立てていくのが研究者として最も重要な部分です。
正しく理解して研究に臨んでください。
また、研究を行うにはある程度のパソコンのスペックが必要です。
ノートパソコンの記事も書いていますので、そちらも見てみてください。
この記事が相関係数で困っている人の役に少しでも立てれば嬉しく思います。
スポンサーリンク
