スポンサーリンク
解決したい悩み
-
3群以上のグループの比較の方法が分からない
-
適切な統計手法の選択がしたい
-
分散分析についての正しい知識を身につけたい
研究を始めたばかりの人がもっともつまづくのが統計手法についてではないでしょうか。
研究で明らかにしたいことははっきりしていても、それを証明するためにはどのようの研究手法を選べば良いのか分からないという人も多いと思います。
特に3グループ以上の比較になると複雑な検定名なども出てきて、頭が混乱してしまいますね。
この記事では3グループ以上の比較を行う方法が知りたい、分散分析の正しい知識を身につけたいという人に向けて、分散分析の考え方と分散分析の選び方、その後の多重比較の方法を分かりやすく解説していきます。
この記事を読むことで、分析の選び方が理解でき、統計ソフトで簡単に検定ができるようになります。
統計の悩みはさくっと解決して、スムーズな研究遂行をしていきましょう。それでは解説していきます。
関連する記事一覧
統計について勉強している人は以下の記事で初心者向けの統計に関する書籍も紹介していますので、そちらもぜひ読んでみてください。今回解説している分散分析についても理解も深まると思いますよ。
あわせて読みたい
分散分析とは
分散分析とは、比較したいグループが3つ以上ある場合に選択される統計手法で、3グループの間のデータに差があるかどうかを検定していきます。分散分析では、帰無仮説を「3群間の平均値(順位)に差がない」と設定し、対立仮説を「3群間の平均値(順位)に差がある」とします。
そのため、分散分析でp＜0.05であれば、帰無仮説は棄却され、3群間に差があることが証明されます。
p値や帰無仮説、対立仮説については過去の記事「【p値とは？有意差とは？】統計用語の基礎知識を分かりやすく解説！！」も参考にしてください。
ここで注意する点は、あくまで3群間のいずれかに差があるということだけが分かるということです。
実際にどの群とどの群に差があるかは分散分析の結果だけでは分かりません。
ここからさらに多重比較(post hoc test)を行うことで、どの群間に差があるのかを明らかにしていく必要があります。
その他の2群間の統計手法の選び方は過去の記事「【t検定の選び方】対応のある？対応のない？適切な選び方を徹底解説！！」と「【差の検定】統計手法の選び方を数式を一切使わず分かりやすく解説します！！」も参考にしてください。
分散分析の選び方
実際に分散分析の手法を選択していくにあたっては、以下の2点を考える必要があります。-
対応の有無
-
正規性の有無
対応があるデータとは、同じ対象から収集されたデータのことであり、反対に対応のないデータとは異なる対象から収集されたデータのことです。
例えば、1つのクラスの1学期のテストの結果と2学期のテストの結果を比較する場合は対応のあるデータ、A組とB組のテストの結果を比較する場合は対応のないデータとなります。
対応の有無に関しては「【t検定の選び方】対応のある？対応のない？適切な選び方を徹底解説！！」の記事の中で詳しく解説していますので、そちらも参考にしてみてください。
また、正規性については、尺度水準で考えたり、実際に正規性の検定を行うことで検証を行ったりします。
尺度水準と正規性についても、過去に詳しく解説をしていますので、そちらを参考にしてください。
さて、ここまでで自分のデータが対応のあるデータかないデータか、正規性のあるデータかないデータかが判別できたと思います。
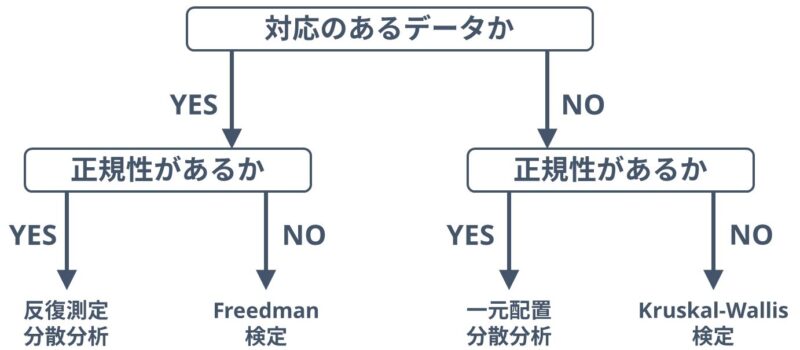
あとはそれぞれを以下のフロー表に当てはめて統計手法を選択してください。
このフロー表を見ると、対応のあるデータで正規分布している場合は反復測定分散分析、対応のないデータで正規分布していない場合にはKruskal-Wallis検定を行えば良いことが分かります。
多重比較
分散分析の選び方は分かりましたが、分散分析を行うだけでは、3グループ以上の比較は不十分です。なぜなら、先ほども言いましたが、分散分析ではいずれかに差があるのは分かるけど、どことどこに差があるのかは分からないからです。
そのため、分散分析で有意差が確認できた場合は、その後の検定として多重比較を行う必要があります。
多重比較法にはTukey法やDunnet法、Steel-Dwass法などがありますが、ここではもっとも汎用性の高い、Bonferroni法を紹介します。
Bonferroni法によるp値の補正
Bonferroni法は最も一般的な多重比較の方法で、手計算でも実施可能なp値の補正法です。
方法は簡単で、それぞれの群間の2群間比較の結果で得られたp値に検定の合計回数をかけることでp値を補正します。
適切な2群間比較の手法さえ選択できれば、Bonferroni法自体は、全ての分散分析の多重比較法として使用できます。
では、具体例を挙げて説明していきます。
A組とB組とC組のテストの平均点を一元配置分散分析で比較した結果、有意差が得られたため、多重比較を行ったとします。この時、各群間で対応のないt検定を行った結果以下のような結果が得られました。
- A組 vs B組 p=0.01
- B組 vs C組 p=0.02
- A組 vs C組 p=0.015
一見すべての群で有意差が出ているように見えますが、ここでBonferroni法を用いて、p値を補正します。
検定は「A組vsB組」、「B組vsC組」、「A組vsC組」の3回実施しているので、それぞれのp値に3をかけます。
- A組 vs B組 p=0.01×3=0.03
- B組 vs C組 p=0.02×3＝0.06
- A組 vs C組 p=0.015×3＝0.045
これで多重比較は終了です。
この結果で得られた補正されたp値から、A組とB組間、A組とC組間に有意差があることが分かりました。
なぜ多重比較法が必要なのか
ここからは少し理論的な話になります。
なぜ、多重比較では2群間比較を繰り返し行うだけではダメなのかについてです。
これには検定の多重性の問題が関わってきます。
検定の多重性とは検定を繰り返し行うことで、αエラーが増大すること
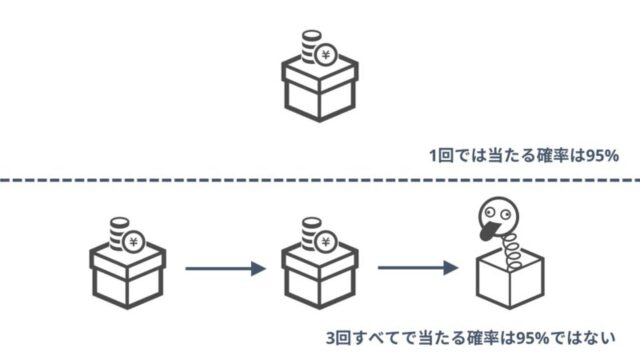
p＜0.05を有意とした場合、帰無仮説が棄却され、対立仮説が支持される確率は95%です。
しかし、検定を3回繰り返した場合、95%が3回連続で的中する確率は0.95×0.95×0.95で約85%となってしまいます。
すなわち、15%の確率でどれか一つは間違えてしまうという問題が生じてしまいます。
95%の確率で当たるくじが3回連続で当たる確率は95%じゃないですよね。それと同じ考え方です。
このような問題を解決するためにp値を補正して、トータルで95%が的中するように補正しているのが多重比較法です。
分散分析の必要性
実は分散分析は3グループ以の比較において必要ないのではないかという意見もあります。これは分散分析は行わず、始めから多重比較の手順を行っても目的とする検定結果である差の有無は確認できるのではないかということです。
この点については正しいと僕は考えています。
そもそも分散分析は計算量を省きたいという意図から開発された分析手法です。
今でこそ、すべてソフトが計算してくれますが、昔は細かい計算をすべて手作業で行っていました。
どの群にも差がないのに各群の2群間比較を繰り返して計算する手間を省くために、まず分散分析を行って、差があれば面倒だけど2群間比較を繰り返そうとしたわけです。
分散分析で差がなければ2群間比較の手間が省けますからね。
そのため、分散分析の過程は省いても構いませんし、p値が一つ減る分、研究トータルで見た場合のαエラーは減少するとも思っています。
まとめ
- 分散分析とは比較したいグループが3つ以上ある場合に選択される統計手法
- 分散分析ではグループ間のどこかに差があるかどうかが分かる
- どこに差があるのかは多重比較で明らかにする
- 分散分析は対応の有無と正規性の有無から手法を選択できる
いかがだったでしょうか。今回は分散分析について考え方や分散分析の選び方、多重比較の方法を解説しました。
分散分析を選択する上で特に難しい知識は必要ありませんし、実際の計算はすべて統計ソフトが自動で行ってくれます。
無料で分散分析を行うことのできるソフトも過去記事「【厳選】研究者が本当におすすめする初心者向けの無料統計ソフト3選！！」で紹介していますので、そちらもご覧ください。
また、この記事の中で紹介しているJASPを使って分散分析を行う方法も解説しています。
この記事もぜひ読んでみて下さい。
正しい手法を選ぶことさえできれば、研究は驚くほどスムーズになります。この記事が分散分析で悩んでいる人の手助けになれば幸いです。
スポンサーリンク
