【平均値と中央値について】それぞれの特徴と使い分けを具体例つきで徹底解説！！

どーもー！！ナツです！！
今日はどうしたのー？

データの平均値を出してみたんだけど、なんか現実的じゃない数値が出てきて…
これ本当に合ってるの？

データを分析する際に一番最初に行うことはデータの平均値と標準偏差を算出することではないでしょうか。

平均値はデータを解析、公表する上で最も一般的な数値ですし、パッと見て理解もされやすいと思います。

ところが平均値すべてが実情を正確に表しているとは言いにくい側面があり、場合によっては中央値を使用した方が良い場合もあります。

平均値を使うべきところ、中央値を使うべきところを正しく理解していないと、結果の解釈を誤ってしまうどころか、間違った情報を世間に公表してしまうことだってあります。

ところが意外と平均値と中央値の使い分けが正しくできる人も少ないのではないでしょうか。

この記事ではデータの解釈を正確にしたい人、平均値と中央値の使い分けを正しく行いたい人に向けて、平均値と中央値の基礎知識を小難しい数式なしで解決していきます。

この記事を読めば、平均値と中央値の使い分けを正しく理解することができ、データの解釈に関する十分な知識が身につきます。

また、平均値と中央値の違いを正しく理解することで、その先のステップである統計手法の選択にも役立ちます。

統計手法の選択については以下の記事でも解説していますので、参考にしてみてください。

それでは解説していきます。

【t検定の選び方】対応のある？対応のない？適切な選び方を徹底解説！！ 統計手法の選び方は初心者が必ずつまづくポイントですよね。   統計アレルギーという言葉が生まれるくらい、統計手法は複雑に見え...

統計について勉強している人は以下の記事で初心者向けの統計に関する書籍も紹介していますので、そちらもぜひ読んでみてください。今回解説している平均値や中央値についても理解も深まると思いますよ。

平均値とは文字通り、複数のデータの平均の値です。

平均値はすべての値を足して、データ数で割ったものを言います。

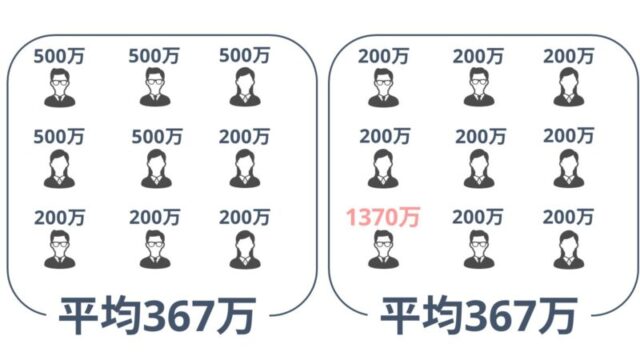
簡単な例を挙げると、貯金額が500万円の人が5人、貯金額が200万円の人が4人いた場合の平均貯金額は

となり、平均値は367万円であることが分かりました。

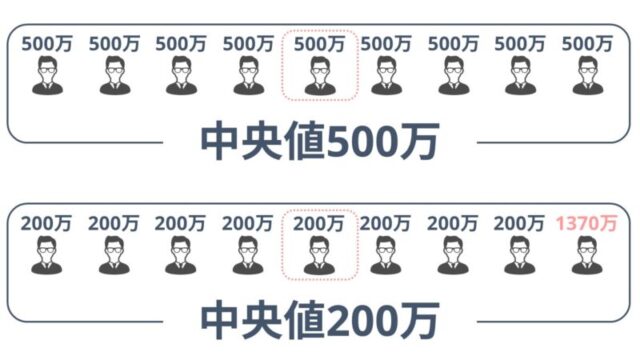
一方、中央値ではこのような計算は必要ありません。中央値はデータを小さい順に並べたとき、真ん中にくる数値のことを指します。

上の5人の500万円貯金している人と4人の200万円を貯金している人を例にとると、

となり、中央値は500万円です。

同じデータなのに、平均値と中央値で約130万円もの差が出てしまいましたね。

この差こそ、平均値と中央値を使い分ける必要がある理由であり、これを理解していないとデータを誤って解釈してしまうことにつながります。

平均値の罠

平均値ではなく、中央値を見る

平均値は怪しいことがあることは理解してもらえたと思います。

では、この平均値の罠に引っかからないためにはどうすれば良いのでしょうか。

平均値と中央値の使い分け