スポンサーリンク
解決したい悩み
「標準偏差って難しそうでよく分からない」
「標準偏差の意味が正しく知りたい」
「Excelで標準偏差の計算がしたい」
統計を行っていて標準偏差ときくと難しいと感じてしまう人も多いのではないでしょうか。
調べてみると複雑な計算式がたくさん出てきて、心が折れかけている人もいるかもしれませんね。
実は標準偏差は全く難しいことなく、むしろ簡単に理解できて、すぐに研究に役立つ知識です。
この記事では、標準偏差が難しくてよく分からない、計算方法が知りたいという人に向けて、標準偏差の意味や必要性、Excelを用いた計算方法を解説していきます。
この記事を読めば、標準偏差の正しい知識を得ることができ、簡単に標準偏差が算出できるようになります。
それでは解説していきます。
関連記事一覧
統計について勉強している人は以下の記事で初心者向けの統計に関する書籍も紹介していますので、そちらもぜひ読んでみてください。今回解説している標準偏差についても理解も深まると思いますよ。
あわせて読みたい
Contents
標準偏差とは何か
 標準偏差とは英語ではStandard Deviationと表記され、SDと略されます。
標準偏差とは英語ではStandard Deviationと表記され、SDと略されます。標準偏差とはデータのバラつきを表す数値で、例えば平均身長170±5.0cmと表記されていた場合の±以下の数値のことです。
この例の場合は5.0が標準偏差に該当します。
標準偏差は分散の平方根を取ることで計算されますが、そんなことは研究者にとっては正直どうでも良いものです。
今はExcelで自動で計算してくれるので、それよりも標準偏差の意味や捉え方、解釈などを理解しておく方が100倍大切だと思います。
標準偏差の意味
 標準偏差はデータのバラつきを表す数値であると説明しました。
標準偏差はデータのバラつきを表す数値であると説明しました。でも「データのバラつきって具体的になに?」と言われれる方もいるかもしれません。
標準偏差について一番理解しておいてほしいことは
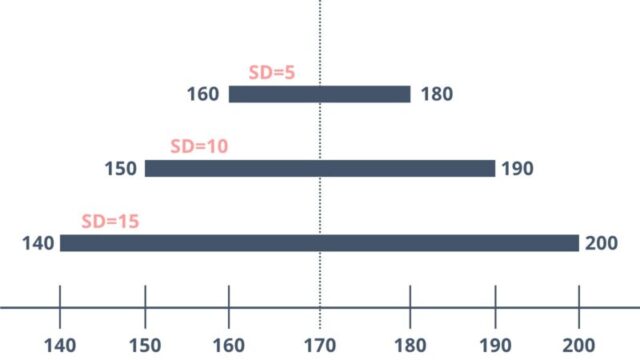
平均値±1SDにデータがある確率が68%、平均値±2SDにデータがある確率が95%
ということです。
具体例を挙げると、平均身長170±5.0cmの集団がいたとすると、165cm~175cmの間にデータの68%が、160cm~180cmの間にデータの95%が収まると解釈できます。
つまり、この研究で対象とした人の身長はほぼ160cm~180cmであると理解することができます。
なぜ標準偏差が必要なのか
 標準偏差はデータの分布を理解するために必要な数値です。
標準偏差はデータの分布を理解するために必要な数値です。標準偏差を理解せずに、平均値だけを見ているとデータの誤認が生まれてしまう可能性があります。
このように標準偏差が大きくなれば当然ですがデータの分布は広くなります。
あまりに標準偏差が大きいデータの場合は、平均値に対してあまりに小さい(大きい)値を含んでいて、平均値を歪めている可能性も考えられます。
このような値を外れ値と言いますが、標準偏差を確認することで外れ値の有無にも気づけるようになります。
また、標準偏差が大きいデータでは検定にかけたときには有意差が出にくくなります。これも、データの分布が広くなるので当然ですね。
標準偏差の注意点
 標準偏差には注意する点は以下の2つです。
標準偏差には注意する点は以下の2つです。
-
平均値とセットで使う
-
データが正規分布していることが前提である
平均値とセットで使う
標準偏差とは平均値に対するデータのバラつきに関する数値なので必ず平均値とセットで使用してください。
データの代表値には平均値のほかに中央値や最頻値などがありますが、それらとともに標準偏差を使用することはできません。
ちなみに平均値の次によく使われる中央値の場合は四分位範囲という数値でデータのバラつきを示します。
平均値と中央値の違いについては過去の記事「【平均値と中央値について】それぞれの特徴と使い分けを具体例つきで徹底解説!!」を参考にしてみて下さい。
データが正規分布していることが前提である
標準偏差を参考にしてよいのはデータが正規分布していることが前提になっています。
先ほどからも解説していますが、データが正規分布していない場合は標準偏差が大きくなってしまいます。
これは、データの偏りや外れ値が原因となりますが、標準偏差が大きすぎる場合はデータの信憑性が低下し、果ては統計にかけたときの解析結果も疑わしくなります。
また、正規分布していない場合は天井効果やフロア効果が出現する可能性も高くなります。
正規分布について詳しく知りたい方は過去の記事「【正規性とは?】正規分布の特徴や統計に関わる考え方を数式なしで分かりやすく解説!!」を参考にしてください。
また、天井効果とフロア効果についても「【天井効果とフロア効果】その意味と起こる原因、対策までどこよりも分かりやすく解説します!!」で解説していますので、そちらも参考にしてください。
Excelで標準偏差を計算する方法
 ここからはExcelで標準偏差を計算する方法を解説していきます。
ここからはExcelで標準偏差を計算する方法を解説していきます。まず、前提としてExcelには標準偏差を計算するための関数が4種類あります。
-
STDEV.P関数
-
STDEVP関数
-
STDEV.S関数
-
STDEV関数
このうち、STDEV.P関数とSTDEVP関数、STDEV.S関数とSTDEV関数はエクセルのバージョンの違いだけです。
Excel2010以降の人はSTDEVP関数とSTDEV関数のいずれかを使用してください。それぞれの関数の違いは以下の通りです。
【STDEVP関数】
母集団全体の標準偏差を計算する関数です。社内アンケートなどで全数調査ができている場合にはこちらの関数を使用します。
【STDEV関数】
母集団から抜き出した標本の標準偏差を計算する場合に使用する関数です。研究の過程で標準偏差を計算する場合はほとんどがこちらの関数を使用することになると思います。
母集団や標本の概念については「【サンプルサイズの決め方】基礎知識や必要性、無料の計算ソフトについて分かりやすく解説!!」の記事の中でも解説していますので、そちらも参考にしてみて下さい。
STEP1:データを入力したシートを用意する
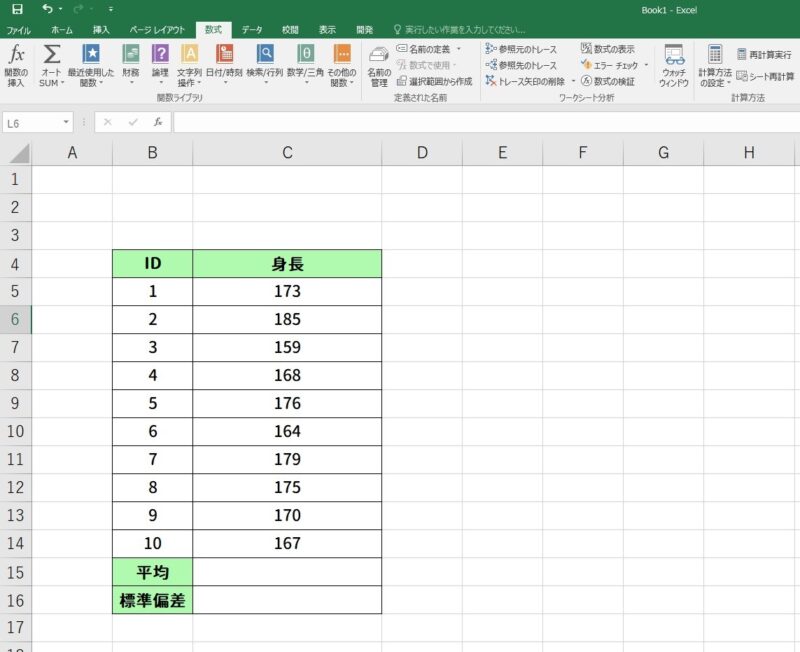
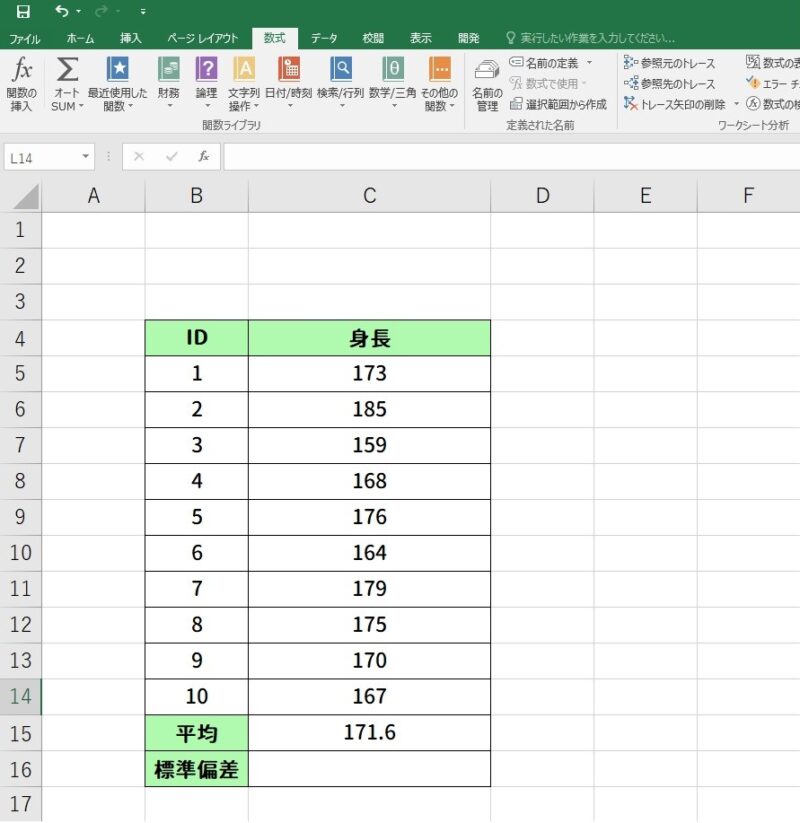
今回は10名の身長の平均値と標準偏差を求めてみます。データを入力したシートはこのようになります。
この時、データは各行に個人IDとデータが並ぶように配置してください。この場合は身長のデータが縦に並ぶように入力するということです。
STEP2:平均値を求める
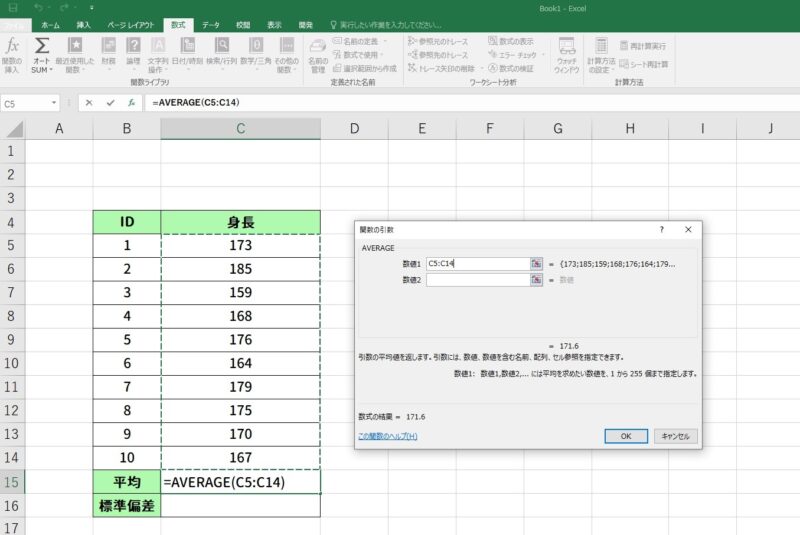
平均値を求めるにはAVERAGE関数を使用します。
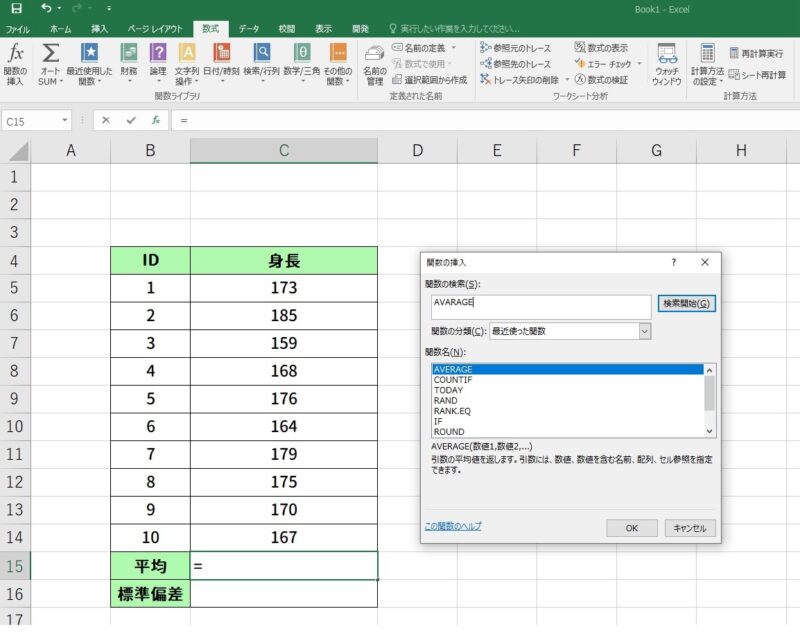
平均値を入力したいセルを選択して「数式」タブから「関数挿入」を選択して、検索窓に「AVERAGE」と入力して検索をかけます。
その後、一番上に表示された「AVERAGE」をクリックしてください。
続いて、平均値を求めるセルの範囲を選択します。直接入力しても結構ですし、ドラッグで選択することもできます。
ここでENTERキーを押すと無事に平均値が出力されました。
STEP3:標準偏差を求める
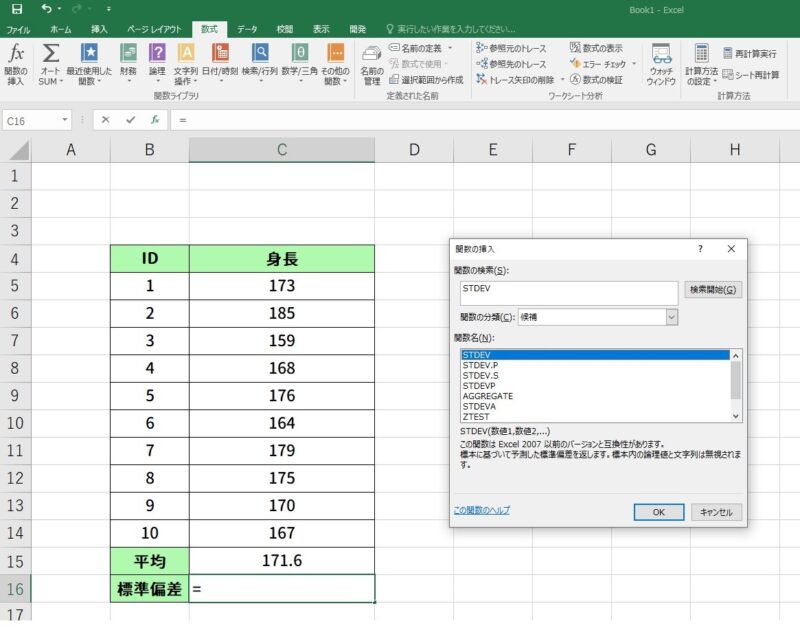
続いて、標準偏差を求めるためにSTDEV関数を使用してみます。
標準偏差を入力したいセルを選択して「数式」タブから「関数挿入」を選択して、検索窓に「STDEV」と入力して検索をかけます。
その後、一番上に表示された「STDEV」をクリックしてください。
続いて、標準偏差を求めるセルの範囲を選択します。直接入力しても結構ですし、ドラッグで選択することもできます。
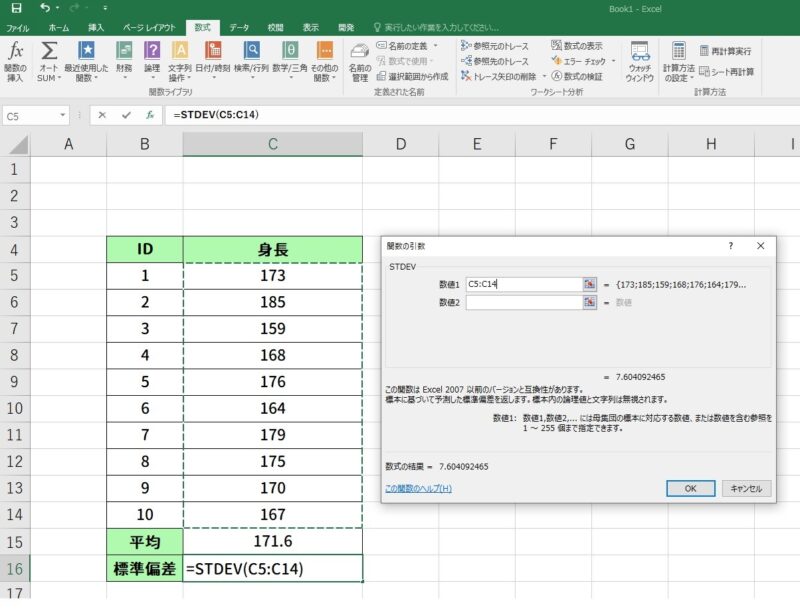
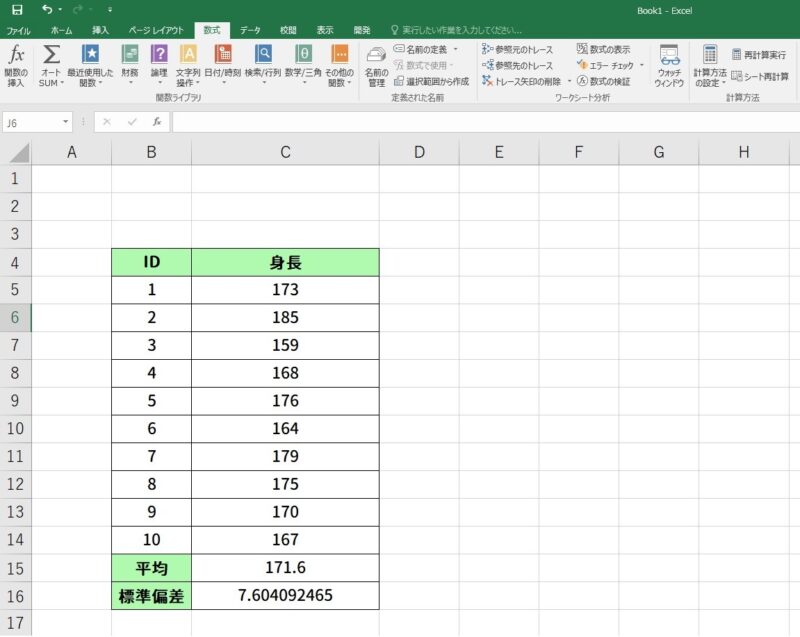
ここでENTERキーを押すと無事に標準偏差が出力されました。
ここまでで無事に平均値と標準偏差を計算することができました。
このデータは平均身長171.6±7.6と表記することができることが分かりました。
まとめ
-
標準偏差とはデータのバラつきを表す数値
-
標準偏差はデータの分布を理解するために必要
-
標準偏差を参考にしてよいのはデータが正規分布していることが前提
- 標準偏差はExcelで簡単に計算できる
いかがだったでしょうか。今回は標準偏差の意味や注意点、Excelでの計算方法を解説しました。
標準偏差は研究成果を公表する際には平均値と合わせて報告することが必須です。
また、論文を読む際に必ず出現する数値でもあります。
ところが正しく理解していないとデータ誤認を引き起こしたり、無駄に手間取ったりしてしまうかもしれません。
この記事が標準偏差に疑問を持っている人の手助けになればうれしく思います。
スポンサーリンク